The Bayesian Islamic Dilemma

Published on: October 25, 2025

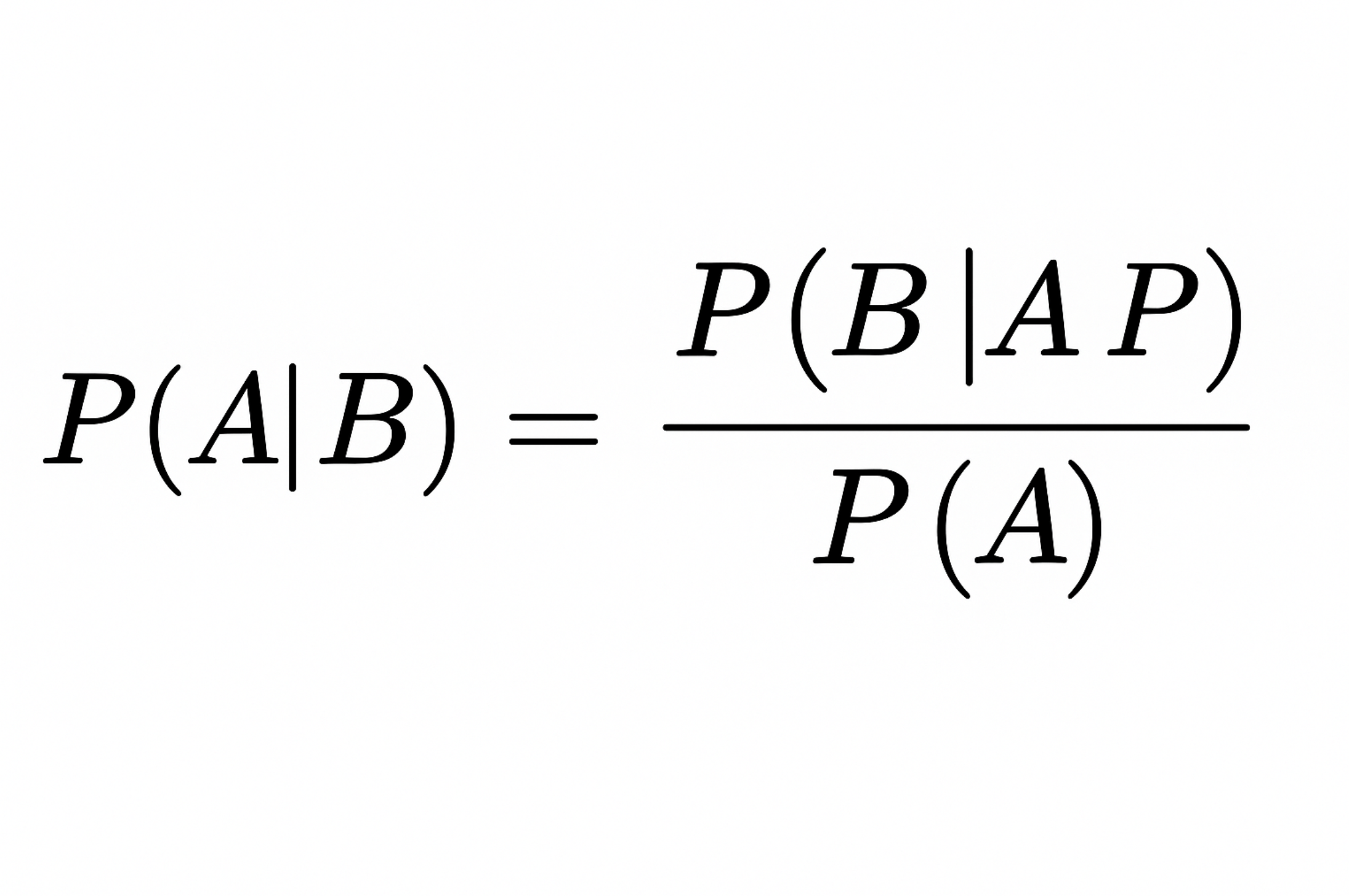
The Bayesian Islamic Dilemma

Inspiring Philosophy Apologetics Roadshow

At this point, you've probably heard about the Islamic Dilemma:

If the Bible is the word of God, Islam is false.
If the Bible is not the word of God, Islam is still false.

This video introduces the Bayesian Islamic Dilemma, using probability theory to show how Islam collapses under its own weight when we analyze the claims of the Qur’an and the Bible.

---

Bayes’ Theorem Overview

The argument relies on Bayes’ Theorem, which expresses how we update our beliefs based on evidence.

1. Standard (Probability) Form

$$P(H \mid E, K) = \frac{P(E \mid H, K) \times P(H \mid K)}{P(E \mid K)}$$

Where:

• $H$ = Hypothesis (Christianity or Islam)
• $E$ = Evidence
• $K$ = Background knowledge
• $P(H \mid K)$ = Prior probability
• $P(E \mid H, K)$ = Likelihood (how well the hypothesis explains the evidence)
• $P(H \mid E, K)$ = Posterior probability (our updated belief after seeing the evidence)

---

2. Odds Form of Bayes’ Theorem

The odds form makes comparison between two hypotheses more intuitive:

$$\frac{P(C \mid E, K)}{P(I \mid E, K)} = \frac{P(C \mid K)}{P(I \mid K)} \times \frac{P(E \mid C, K)}{P(E \mid I, K)}$$

Where:

• $C$ = Christianity
• $I$ = Islam
• Left side → Posterior Odds (after seeing the evidence)
• First term → Prior Odds (starting belief before evidence)
• Second term → Likelihood Ratio (how much the evidence favors one side)

---

Step-by-Step Example from the Video

Example 1: Priors Favoring Christianity

$$P(C \mid K) = 0.99, \quad P(I \mid K) = 0.01$$

So the prior odds are:

$$\frac{0.99}{0.01} = 99$$

If the evidence (the “Islamic Dilemma”) is 2000× more likely under Christianity than under Islam, the likelihood ratio is:

$$\frac{P(E \mid C, K)}{P(E \mid I, K)} = 2000$$

The posterior odds then become:

$$99 \times 2000 = 198{,}000$$

Converting to probability:

$$P(C \mid E, K) = \frac{198{,}000}{198{,}000 + 1} \approx 0.999995$$

That’s 99.9995% for Christianity vs. 0.0005% for Islam.

---

Example 2: Priors Favoring Islam

$$P(C \mid K) = 0.01, \quad P(I \mid K) = 0.99$$ $$\frac{P(C \mid K)}{P(I \mid K)} = \frac{1}{99}$$

Keeping the same likelihood ratio (2000):

$$\text{Posterior Odds} = \frac{1}{99} \times 2000 = 20.2$$ $$P(C \mid E, K) = \frac{20.2}{20.2 + 1} \approx 0.953$$

Even with Islam’s prior set at 99%, Christianity still comes out at 95.3% posterior probability.

---

Intuitive Summary

Factor	Christianity	Islam
Prior (starting)	1% or 99%	99% or 1%
Likelihood (fit with evidence)	~0.8	< 0.0004
Posterior (after evidence)	≈ 95–99.999%	≈ 0–5%

Even when Islam is given overwhelming prior advantage, the evidence (“status” + “content” of the Bible and Qur’an) flips the odds decisively in favor of Christianity.

---

Key Equations Recap

1. Posterior Odds Form

$$\text{Posterior Odds} = \text{Prior Odds} \times \text{Likelihood Ratio}$$

2. Posterior Probability Conversion

$$P(C \mid E, K) = \frac{\text{Posterior Odds}}{1 + \text{Posterior Odds}}$$

---

Summary of Submodels (Islam)

Submodel	Description	Outcome
Islam₁ – Affirmation	Qur’an affirms Torah and Gospel as intact.	Collapses due to contradiction (affirms texts that refute Islam).
Islam₂ – Corruption	Torah/Gospel textually falsified.	Collapses under Qur’anic language and early tafsir evidence.
Islam₃ – Lost Injil Hypothesis	Qur’an refers to a lost gospel.	Collapses under historical, manuscript, and theological implausibility.

Each submodel collapses either by contradiction, incoherence, or historical falsification — leaving Islam with near-zero total likelihood under Bayesian analysis.

---

Conclusion

Even when Islam is granted every numerical advantage — 99% prior probability, maximal interpretive charity, and upper-bound likelihoods — the Bayesian Islamic Dilemma shows that:

$$P(E \mid C, K) \gg P(E \mid I, K)$$

That is, the evidence is thousands of times more probable if Christianity is true than if Islam is true.

The result:

$$\text{Posterior Odds} = 20:1 \text{ or higher in favor of Christianity}$$

This demonstrates mathematically that Islam’s own internal structure and textual claims collapse under Bayesian scrutiny.

---

References

1. Bayes, Thomas. An Essay towards Solving a Problem in the Doctrine of Chances. Philosophical Transactions of the Royal Society of London, 1763.
2. Earman, John. Bayes or Bust? A Critical Examination of Bayesian Confirmation Theory. MIT Press, 1992.
3. McGrew, Timothy, and Lydia McGrew. “The Argument from Miracles: A Cumulative Case for the Resurrection of Jesus of Nazareth.” In The Blackwell Companion to Natural Theology, 2009.
4. Nicholson, Gordon. The Quranic View of the Biblical Text: Early Tafsir and the Development of the Doctrine of Tahrif. Oxford Islamic Studies, 2018.
5. David Wood. The Bayesian Islamic Dilemma (YouTube presentation).
6. Jonathan McLatchie. “The Bayesian Case for Christianity.” Apologetics Academy, 2021.
7. N. T. Wright. The Resurrection of the Son of God. Fortress Press, 2003.
8. William Lane Craig. Reasonable Faith: Christian Truth and Apologetics. Crossway, 2008.
9. Ali Ataie. “The Qur’an and the Bible: A Historical Textual Comparison.” Zaytuna Institute Lecture Series, 2015.
10. Plantinga, Alvin. Warranted Christian Belief. Oxford University Press, 2000.